
Zadanie Klub Prawoskrętnych Kierowców (kpk)
Pomóż nam usprawnić bazę zadań!
Klub Prawoskrętnych Kierowców
Limit pamięci: 32 MB
Dana jest prostokątna mapa miasta złożona z  kwadratowych
pól (
kwadratowych
pól ( i
i  ). Wiersze
kwadratowych pól tworzących mapę są ponumerowane kolejno od góry do dołu
liczbami od
). Wiersze
kwadratowych pól tworzących mapę są ponumerowane kolejno od góry do dołu
liczbami od  do
do  , a kolumny od lewej do prawe, kolejno
od
, a kolumny od lewej do prawe, kolejno
od  do
do  . Każde pole jest albo wolne albo zablokowane.
Ruch kołowy jest dozwolony tylko po wolnych polach. Z każdego wolnego pola można
przejechać na wolne pole przyległe (tzn. takie, które ma z danym polem wspólny
bok), nie można jednak zawracać, to znaczy bezpośrednio po przejechaniu z pola
. Każde pole jest albo wolne albo zablokowane.
Ruch kołowy jest dozwolony tylko po wolnych polach. Z każdego wolnego pola można
przejechać na wolne pole przyległe (tzn. takie, które ma z danym polem wspólny
bok), nie można jednak zawracać, to znaczy bezpośrednio po przejechaniu z pola
 na przyległe pole
na przyległe pole  wrócić na
wrócić na  .
.
Klub Prawoskrętnych Kierowców złożył zamówienie na program komputerowy, który
dla dowolnych dwóch różnych pól  oraz
oraz  rozstrzyga, czy
można dojechać od punktu
rozstrzyga, czy
można dojechać od punktu  do
do  nie wykonując ani jednego
skrętu w lewo, a jeśli tak, znajduje jedną taką drogę o minimalnej długości.
Długość drogi jest to liczba wszystkich jej pól. Do drogi od
nie wykonując ani jednego
skrętu w lewo, a jeśli tak, znajduje jedną taką drogę o minimalnej długości.
Długość drogi jest to liczba wszystkich jej pól. Do drogi od  do
do
 zaliczamy również pola
zaliczamy również pola  oraz
oraz  .
.
Zadanie
Ułóż program który:
- wczytuje ze standardowego wejścia dane o prostokątnej sieci pól (tzn.
liczbę wierszy
 , liczbę kolumn
, liczbę kolumn  i stan każdego pola, a
następnie współrzędne dwóch różnych pól
i stan każdego pola, a
następnie współrzędne dwóch różnych pól  i
i  ;
; - rozstrzyga, czy istnieje droga bez skrętów w lewo od pola
 do
do
 i jeśli nie, to zapisuje w standardowym wyjściu jedno słowo
NIE, a jeśli tak, to znajduje jedną taką drogę o minimalnej długości i
zapisuje ją w standardowym wyjściu. Jeśli chociaż jedno z pól
i jeśli nie, to zapisuje w standardowym wyjściu jedno słowo
NIE, a jeśli tak, to znajduje jedną taką drogę o minimalnej długości i
zapisuje ją w standardowym wyjściu. Jeśli chociaż jedno z pól  ,
,
 nie jest wolne, to odpowiedzią jest NIE.
nie jest wolne, to odpowiedzią jest NIE.
Wejście
W standardowym wejściu znajdują się dwie liczby całkowite, oddzielone
pojedynczym odstępem: liczba wierszy  oraz liczba kolumn
oraz liczba kolumn
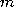 . W każdym z kolejnych
. W każdym z kolejnych  wierszy pliku znajduje się opis
odpowiedniego kolejnego wiersza mapy w postaci jednego słowa o długości
wierszy pliku znajduje się opis
odpowiedniego kolejnego wiersza mapy w postaci jednego słowa o długości
 utworzonego z cyfr
utworzonego z cyfr  i
i  . Cyfra
. Cyfra  oznacza, że odpowiednie pole jest wolne a cyfra
oznacza, że odpowiednie pole jest wolne a cyfra  , że jest
zablokowane.
, że jest
zablokowane.
Następnie w jednym wierszu są zapisane dwie współrzędne pola  oddzielone pojedynczym odstępem: numer wiersza nie większy niż
oddzielone pojedynczym odstępem: numer wiersza nie większy niż  oraz
numer kolumny nie większy niż
oraz
numer kolumny nie większy niż  , a w kolejnym wierszu są zapisane, w
taki sam sposób, dwie współrzędne pola
, a w kolejnym wierszu są zapisane, w
taki sam sposób, dwie współrzędne pola  .
.
Dane w standardowym wejściu są zapisane poprawnie i Twój program nie musi tego sprawdzać.
Wyjście
W standardowym wyjściu należy zapisać:
- albo jedno słowo NIE, gdy nie istnieje droga bez skrętów w lewo od
 do
do  , lub przynajmniej jedno z pól
, lub przynajmniej jedno z pól 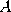 ,
,
 jest zablokowane,
jest zablokowane, - albo opis jednej drogi bez skrętów w lewo od
 do
do  o
minimalnej długości; w tym przypadku w pierwszym wierszu należy wpisać długość
drogi
o
minimalnej długości; w tym przypadku w pierwszym wierszu należy wpisać długość
drogi  , a w każdym z kolejnych
, a w każdym z kolejnych  wierszy dwie współrzędne
kolejnego pola drogi oddzielone pojedynczym odstępem.
wierszy dwie współrzędne
kolejnego pola drogi oddzielone pojedynczym odstępem.
Przykłady
Dla danych wejściowych:
8 9 010011101 011010101 000000000 111010101 101000100 111010101 000000000 101011111 2 6 1 3
poprawną odpowiedzią jest:
NIE
Dla danych wejściowych:
8 9 010011101 011010101 000000000 111010101 101000100 111010101 000000000 101011111 2 6 3 8
poprawną odpowiedzią jest:
12 2 6 3 6 4 6 5 6 5 5 5 4 4 4 3 4 3 5 3 6 3 7 3 8
Autor zadania: Piotr Chrząstowski-Wachtel.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English